Post experimental

Hello my friends, stay awhile and listen!

Primeiro post \o/. Esse é um tema no qual coincidentemente esbarrei enquanto também esbarrava no belo e amigável ‘beautiful-jekyll’. Combinação de coincidências que me fez (finalmente) começar a escrever.

Vamos a questão, recentemente me uni a um grupo de Devs e nossa primeira brincadeira oficial está sendo trabalhar com uma base de dados de preços de casas que consiste em algumas centenas de linhas e 80 variáveis. Depois de desbravar um pouco a base,observamos multicolinearidade (vulgo : alguns preditores são muito semelhantes entre si ) então surgiram as ideias de como lidar. Criar uma outra variável que contenha informação de ambas e dropar as originais depois? Dropar uma e deixar outra? Se sim, qual dropar? Estamos viajando e na verdade não precisa mexer em nada disso? Como saber o que é melhor?

Existem várias formas de decidir e a primeira que me veio a mente foi o teste da razão de verossimilhança, mas como se trata de um post sobre como tomar essa decisão, vamos colocar mais algumas formas de como chegar a ela. Sempre de forma mais intuitiva, simples e direta que minha habilidade de comunicação permitir. Antes de seguir, vale ressaltar que existe uma discussão sobre ‘multicolinearidade é motivo suficiente para se livrar de uma variável?’, como tudo na Estatística e suas versões gourmet a resposta é depende, então sempre que houver um tema importante, mesmo que eu não avise, provavelmente tem uma discussão interminável nos bastidores. Para prosseguir sem consciência pesada, vamos convenientemente supor que ‘sim, multicolinearidade é motivo suficiente para se livrar de uma variável’.

Saber qual a melhor versão do modelo, de acordo com as alterações sugeridas acima, é uma ótima forma de decidir qual a melhor alteração a se fazer. Então eis aqui algumas métricas para este fim:

• AIC

  AIC = 2k - 2ln()

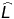O critério de informação de Akaike é uma métrica de qualidade de modelo. ‘k’ é o número de variáveis no modelo e ‘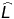’ é a máxima verossimilhança do modelo (que é de forma resumida, um valor que representa o quão bem o meu modelo explica os dados, vamos falar disso em outro post). O que acontece com essa métrica quando dropamos variáveis é que diminuimos o valor de ‘k porém também diminuímos ‘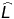’ porque certamente nosso modelo vai ficar um pouco pior em explicar os dados. Observe que pela fórmula do AIC, o menor valor possível significa o melhor modelo possível, então se você dropa uma variável e de repente seu AIC que era -1000 passou para -800, é sinal de que você não deveria estar dropando tal variável. Por outro lado se o AIC ficar ainda menor ou se a diferença é ínfima (de -1000 para -990 por exemplo), é sinal de que o drop da variável é aceitável.

• BIC

  BIC = ln(n)k - 2ln()

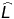O critério de informação Bayesiano é bastante parecido com o AIC, e é avaliado da mesma forma, quanto menor melhor. A diferença na fórmula é que o ‘2’ é substituido por ln(n) onde n é o numero de observações, ou seja, o BIC é melhor em penalizar a complexidade do modelo. Em geral a análise do AIC concorda com a do BIC, quando elas discordam o comum é que o AIC esteja indicando que versões mais complexas são melhores. No fim das contas, se você decidir que um deles é interessante para seu caso, o sábio é usar os dois. Se esses carinhas mais simples chamaram sua atenção, aqui está um breve post abordando AIC vs BIC, onde inclusive eles fazem a ousada afirmação de que sua maior referência deve ser o AIC se um falso negativo é um problema mais grave para você, e BIC caso contrário. Fiquem a vontade para investigar e decidir se concordam com isso.

• Cross-Validation

Cross-validation é um método que costuma ser aplicado em observações (ou instâncias) e consiste em dividir o banco em partes iguais, de modo que as variáveis em cada ‘fatia’ do banco estejam distribuídas da mesma maneira. Então separa uma dessas fatias, treina o modelo usando todas as outras observações e então testa usando a parte que você separou, repetindo o processo até que se tenha usado todas as fatias do banco como teste, deste modo é possível prever o erro do modelo de forma mais consistente. (existem variações do cross-validation, a que foi descrita aqui se chama ‘leave-one-out’).

Usando este raciocínio, é possível fazer o leave-one-out com as variáveis, comparando a taxa de erro dos modelos com este mesma taxa calculada utilizando o banco de treino completo. Isso é bem parecido com o que é preciso fazer quando queremos usar o AIC ou BIC como métricas, porém o Cross-validation é mais indicado para uma ‘busca as cegas’.

• Likelihood Ratio Test

  LR = -2[ln(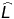0)- ln()]

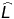O teste da razão da verossimilhança (LR), como o nome sugere, compara os valores da máxima verossimilhança dos modelos. Para entender melhor o que está acontecendo vamos admitir que 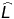0 é a máxima verossimilhança calculada com o modelo completo e 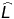é a mesma métrica calculada depois que o modelo sofre a alteração que se quer testar. Multiplicar essa diferença por -2 permite que a métrica seja associada a uma distribuição qui-quadrado, logo para chegar a uma conclusão sobre os modelos, LR é comparado a um certo valor. Este tal valor é retirado da distribuição qui-quadrado e compara-lo com LR equivale a executar um teste de hipótese, onde a hipótese 0 é que não há evidências de que os modelos tem performances diferentes.

Sim, explicar à fundo o LR é um pouco tricky, precisaríamos ainda chafurdar um pouco em teste de hipótese, em entender o básico da distribuição qui-quadrado e saber o que acontece no cálculo da máxima verossimilhança. Felizmente, mesmo que o LR não seja o mais amigável dos métodos, graças a softwares como o R não é necessário implementar o teste, apenas compreender o que acontece por trás dele. Se mesmo assim agora você quer saber o que diabos acontece no cálculo da máxima verossimilhança, ou você não se conforma porque eu não falei mais sobre o valor com o qual LR é comparado no fim das contas, você pode clicar aqui e aqui.

A presto!